In geometry, the tesseract, also called an 8-cell or regular octachoron, is the four-dimensional analog of the cube, which is in turn the three dimensional analog of the square. The tesseract is to the cube as the cube is to the square; or, more formally, the tesseract can be described as a regular convex 4-polytope whose boundary consists of eight cubical cells.
A generalization of the cube to dimensions greater than three is called a “hypercube”, “n-cube” or “measure polytope”. The tesseract is the four-dimensional hypercube or 4-cube.
According to the Oxford English Dictionary, the word tesseract was coined and first used in 1888 by Charles Howard Hinton in his book A New Era of Thought, from the Greek “τέσσερεις ακτίνες” (“four rays”), referring to the four lines from each vertex to other vertices. Some people have called the same figure a “tetracube”, and also simply a "hypercube" (although a hypercube can be of any dimension).
Geometry
The tesseract can be constructed in a number of different ways. As a regular polytope constructed by three cubes folded together around every edge, it has Schläfli symbol {4,3,3}. Constructed as a 4D hyperprism made of two parallel cubes, it can be named as a composite Schläfli symbol {4,3}x{ }. As a duoprism, a Cartesian product of two squares, it can be named by a composite Schläfli symbol {4}x{4}.
Since each vertex of a tesseract is adjacent to four edges, the vertex figure of the tesseract is a regular tetrahedron. The dual polytope of the tesseract is called the hexadecachoron, or 16-cell, with Schläfli symbol {3,3,4}.
The standard tesseract in Euclidean 4-space is given as the convex hull of the points (±1, ±1, ±1, ±1). That is, it consists of the points:
A tesseract is bounded by eight hyperplanes (xi = ±1). Each pair of non-parallel hyperplanes intersects to form 24 square faces in a tesseract. Three cubes and three squares intersect at each edge. There are four cubes, six squares, and four edges meeting at every vertex. All in all, it consists of 8 cubes, 24 squares, 32 edges, and 16 vertices.
Projections to 2 dimensions
The construction of a hypercube can be imagined the following way:
- 1-dimensional: Two points A and B can be connected to a line, giving a new line AB.
- 2-dimensional: Two parallel lines AB and CD can be connected to become a square, with the corners marked as ABCD.
- 3-dimensional: Two parallel squares ABCD and EFGH can be connected to become a cube, with the corners marked as ABCDEFGH.
- 4-dimensional: Two parallel cubes ABCDEFGH and IJKLMNOP can be connected to become a hypercube, with the corners marked as ABCDEFGHIJKLMNOP.
This structure is not easily imagined but it is possible to project tesseracts into three- or two-dimensional spaces. Furthermore, projections on the 2D-plane become more instructive by rearranging the positions of the projected vertices. In this fashion, one can obtain pictures that no longer reflect the spatial relationships within the tesseract, but which illustrate the connection structure of the vertices, such as in the following examples:
A tesseract is in principle obtained by combining two cubes. The scheme is similar to the construction of a cube from two squares: juxtapose two copies of the lower dimensional cube and connect the corresponding vertices. Each edge of a tesseract is of the same length. A multitude of cubes that are nicely interconnected. The vertices of the tesseract with respect to the distance along the edges, with respect to the bottom point. This view is of interest when using tesseracts as the basis for a network topology to link multiple processors in parallel computing: the distance between two nodes is at most 4 and there are many different paths to allow weight balancing.
Tesseracts are also bipartite graphs, just as a path, square, cube and tree are.
http://en.wikipedia.org/wiki/Tesseract





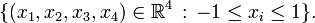










No hay comentarios:
Publicar un comentario